Everything you wanted to know about Coordinate Reference Systems
One day you wake up and you find that you’ve turned into a technician. That was unexpected.
You own a van and you drive around places. This fine day you’re out looking for broken telephone poles in a suburb.
You drive around and find twenty telephone poles. Out of these twenty, you reckon three of them are dodgy, but it’s 3pm and you don’t have time to fix them today.
It’s important for you to be able to find the dodgy poles later, so while you’re at each one you take out your GPS unit and take a reading. Before you clock off for today, you check the history of the GPS unit and write down the three pairs of numbers there:
(151.2092, -33.8684)
(151.2010, -33.8700)
(151.2103, -33.8649)
You sleep easy because you know that with these coordinates written down, you’ll be able to find the poles whenever you like. You know that the coordinates represent longitude and latitude, and that if you plot them on a map you’ll be able to see where the poles are with no dramas.
What you might not realise is that you used a coordinate reference system to find the location of those poles. Coordinate reference systems are used to represent the locations of things on the Earth, and your GPS reciever works by utilising one.
By unwittingingly utilising this coordinate reference system underpinning your GPS receiver, you can easily locate which telegraph poles need fixing.
Nifty.
What is a Coordinate Reference System? Link to heading
A Coordinate Reference System (CRS) is used to uniquely identify the location of things relative to the Earth. It also goes by the name Spatial Reference System (SRS).
Think of the Cartesian plane you studied at school: when you saw a set of coordinates of a point, you instantly knew the exact location of that point. It’s the same thing in the geographical world, just more complicated.
The spatial data you find will be created by using some CRS. Points, lines, polygons, raster sheets - all of this data has to refer to a CRS. It would be meaningless to call it spatial data otherwise.
CRS’s usually come in two categories: geographic and projected. They are heavily related to one another.
Geographic Coordinate Reference Systems Link to heading
In a nutshell: geographic Coordinate Reference Systems define locations using a 3D surface, and measure location with latitude and longitude.
There seems to be a lot of ambiguity surrounding what a geographic CRS is and what it contains. Many sources disagree on the topic and terminology used is often unclear. To keep things consistent I’ll be going by the definitions found on the EPSG website.
With that being said, a geographic CRS is made up of two things:
- A coordinate system
- A datum
Coordinate System Link to heading
The terms “coordinate system” and “coordinate reference system” are often considered as the same thing, but in this context they are different. Here, a coordinate system is a set of axes with their properties (axes, axis names, order, abbreviations etc) and contained within a CRS.
Coordinate systems are classified according to the geometric properties of their coordinate space and of the shape of their axes. They come in a few different forms. Here are a few of them:
- Cartesian coordinate system: position is given assuming the axes are orthogonal and straight. Each axis is measured in the same units.
- Ellipsoidal coordinate system: position is given by latitude, longitude, and optionally height. This coordinate system is the one used in geographic CRS’s.
- Vertical coordinate system: a one dimensional coordinate system that records heights of points above the Earth’s surface.
Datum Link to heading
A datum is used to define a few things: the position of the origin, the scale and the axis orientation of a coordinate system. All these things are defined with respect to an object, which is typically the Earth.
Datums come in different forms. Here are two of them:
- Geodetic datum: defines the model of the Earth to use when calculating coordinates. The model of the Earth is usually an ellipsoid or a sphere. Also contained in the datum is the location and the orientation of the model.
- Vertical datum: describes a reference level surface which is also known as the “zero-height” surface. The position of the zero-height surface with respect to the Earth is also described.
Coordinates only make sense with considered in conjuction with a model of the Earth. The same location on Earth under two different Earth models will be represented by two different sets of coordinates.
WGS 84 Link to heading
One example of a geographic CRS is WGS 84. WGS 84 goes by the EPSG code EPSG 4326 and is one of the most important geographic CRS’s. It is the geographic CRS of choice for the omnipresent GPS system.
(Don’t know how EPSG codes work? Click here.)
Like other geographic CRS’s, WGS 84 is made up of a coordinate system and a datum.
Here is a diagram of the EPSG codes for WGS 84:
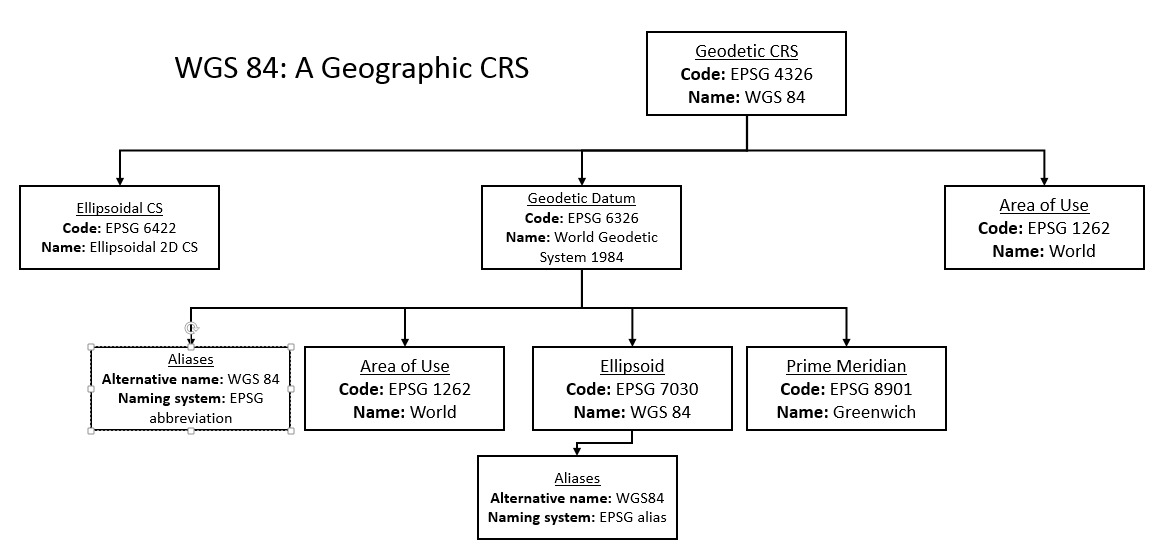
The coordinate system of WGS 84 is an ellipsoidal coordinate system. In this coordinate system position is given by latitude and longitude. The north direction on the latitude axis is taken as positive, and likewise the east direction on the longitude axis is taken as positive.
The datum of WGS 84 is a geodetic datum, going under the EPSG code 6326. This datum models the Earth as an ellipsoid with a semi-major axis radius of 6,378,137m, and an inverse flattening of 298.257223563 (EPSG 7030). The Prime Meridian defines the location and origin of the model. The Prime Meridian is defined as running through Greenwich (EPSG 8901).
This CRS is defined as a 2D CRS, since the ellipsoidal height is not provided in the datum. If it were given, WGS 84 would be a 3D CRS instead.
The EPSG database also defines the area of use for a geographic CRS. While WGS 84 is suitable to be used across the world (EPSG 1262), other geographic CRS’s are only suitable in certain areas.
Projected Coordinate Reference Systems Link to heading
Projected CRS’s can be thought of as the two-dimensional cousin of the three-dimensional geographic CRS. The geographic CRS represents data using a three-dimensional construct; the projected CRS uses projections to transform points from the three-dimensional construct to a two-dimensional map.
Simply put, a projection is a series of transformations that convert the locations of points on a three dimensional surface (defined in the geographic CRS) to locations on a flat surface (defined in the projected CRS).
A projected CRS is made up of three things:
- A geogaphic CRS
- A coordinate system
- A map projection
A geographic CRS uses an ellipsoidal coordinate system; a projected CRS uses a Cartesian coordinate system. A geographic CRS uses latitude, longitude and degrees; a projected CRS uses northings, eastings and metres (or feet, kilometres etc).
Map projection Link to heading
It is difficult to represent a three-dimensional Earth as a two-dimensional map. To mitigate these difficulties a vast number of map projections exist, each with their own strengths and weaknesses.
One way of thinking about a map projection is as a way of converting geographic coordinates (latitude and longitude) into Cartesian coordinates (and vice versa). You could also say that a map projection converts coordinates referenced in a geographic CRS to coordinates referenced in a projected CRS.
For a successful projection you need more than just the name of the map projection. You need projection parameters. These parameters answer questions like:
- Where is the centre of the projection?
- What is the scale factor at each point?
- Where are the standard parallels?
- What are the values of the false easting and false northing?
Let’s look at an example.
NAD83 / Canada Atlas Lambart Link to heading
The NAD83 / Canada Atlas Lambert (EPSG 3978) projection is a projected CRS. This projected CRS uses the geographic CRS known as NAD83 and the map projection Lambert Conic Conformal. The parameters are also provided, including specifiying that this conical projection uses two Standard Parallels.
Here’s the diagram of the EPSG codes for this projected CRS. It’s quite complicated.
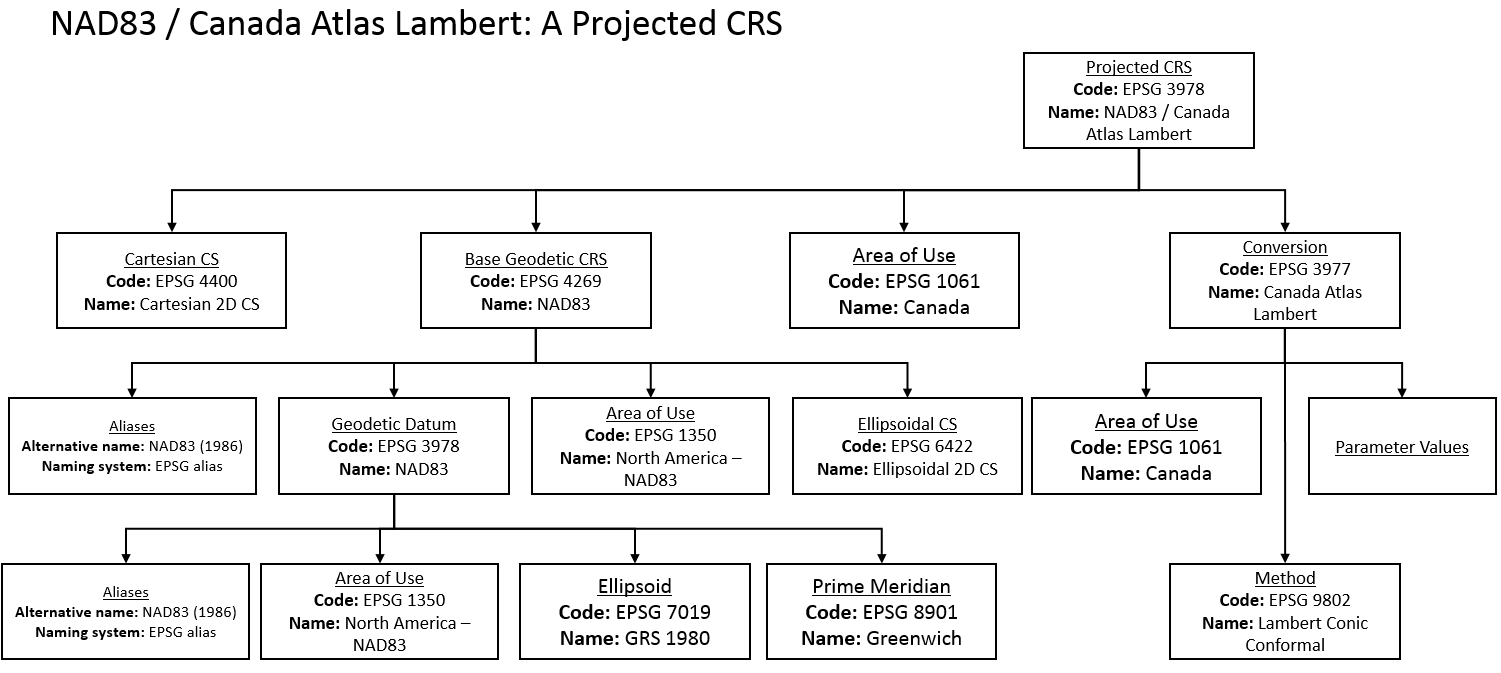
Under the gold-standard EPSG system, a map projection is a subcategory of a “Coordinate Conversion”, or a Conversion for short. Included within the Conversion is a category that details the area of the projection, the conversion method of the projection and the projection parameters.
It’s evident that the projected CRS uses a Cartesian Coordinate system, a geographic CRS and a map projection. You can see that there are two coordinate systems referenced here: the ellipsoidal coordinate system used in the geographic CRS, and the cartesian coordinate system used in the projected CRS.
Conclusion Link to heading
For many applications of spatial data you won’t need to think about what coordinate system it’s referenced as. You’ll put together the layers of data and things will just work.
It’s when things go wrong where you’ll need to dig deeper. Perhaps layers aren’t aligning properly, lakes don’t look right or the position of your data points suspicious - maybe the error can be traced back to a CRS mismatch somewhere.
Or maybe you can’t find those broken telegraph poles again. Probably should have taken a photo.